2022. 11. 9. 17:53ㆍ아티클 | Article/칼럼 | Column
Parametric DesignⅩⅧ
지난 584호 연재에서는 종이접기에 앞서 왜 접는 것인지, 그리고 어떻게 접을 것인지에 대해 생각해 보았고 이를 digital tool로 재해석하기 위한 알고리즘에 대해 개념적인 생각을 전개해 보았습니다. 이번시간에는 이를 토대로 digital model화 하는 과정을 간략하게 살펴보도록 하겠습니다.
가장 먼저 정의해야 했던 부분은 종이를 접는 방향입니다. 먼저 종이를 접는 방향은 두가지가 있습니다. 종이 윗면을 기준으로 접히는 모서리가 위를 향하는 방법과 아래를 향하는 방법이 있습니다. 아래 그림과 같습니다. 즉 초록색 선은 접히는 모서리가 위를 향하고 붉은색 점선은 접히는 모서리가 아래를 향하게 됩니다(Fig. 1).

이에 반해 지난 584호에서 A, B, C를 통해 말하고자 했던 것은 정사각형의 단위 유닛안에서 그 해당 유닛이 접힐 필요가 있는지에 대한 변수화였습니다. 즉 전체적인 시스템이 모두 접혔을 때 표면에 드러나는 면들은 접힐 필요가 없지만 그렇지 않고 드러나는 면들 사이로 시야에서 사라지는 면들은 두 가지 방향성 중 하나의 방향으로 접히게 됩니다. 이를 시계방향과 반시계방향으로 표현했었는데요, 이를 좀 더 명확하게 설명하자면, 하나의 정사각형 유닛에서 centroid를 중심으로 제1사분면의 점을 0번, 시계 방향으로 1, 2 그리고 3번의 점을 정의하면 B의 경우는 0번과 2번의 점을 이어주는 대각선을 중심으로 아래 방향으로 접히게 되고 C의 경우는 1번과 3번의 점을 이어주는 대각선을 중심으로 아래 방향으로 접히게 됩니다(Fig. 2).

그 외의 경우는, 즉 아래 그림에서 초록색 선으로 표현된 부분들은 모두 접히는 모서리가 위를 향하는 방식이라고 생각할 수 있으며 붉은색 점선으로 표시된 선들은 대각선의 방향에 상관없이 접히는 모서리가 아래 방향을 향한다고 할 수 있습니다(Fig. 3).
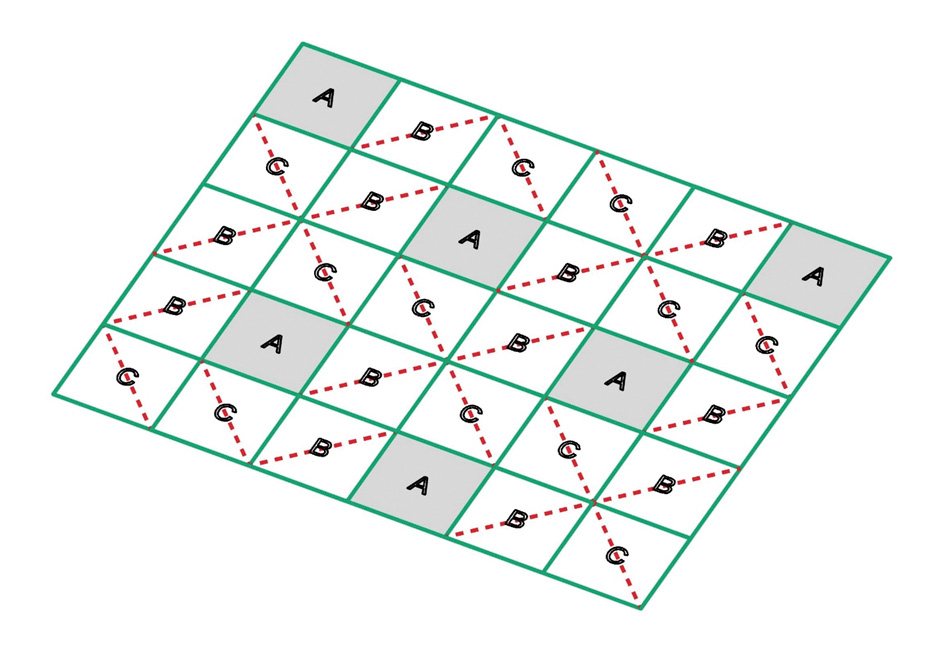
즉 각각의 정사각형 유닛에서 대각선을 따라 접힘이 발생하는지 아닌지에 따라 서로 다른 경우의 수가 발생함을 알 수 있습니다. 여기서 경우의 수를 문자를 이용한 패턴으로 정의함은 추후 parametric tool에게 각 유닛으로부터 패턴에 따른 다른 data set을 추출하도록 명령하기 위함입니다. 다시 말해 두가지의 접힘의 방향(위 / 아래)이 세가지의 단위 유닛에 적용되어야 하며 이를 문자로 이루어진 패턴을 이용해 parametric tool에 전달하는 과정을 거치게 됩니다.
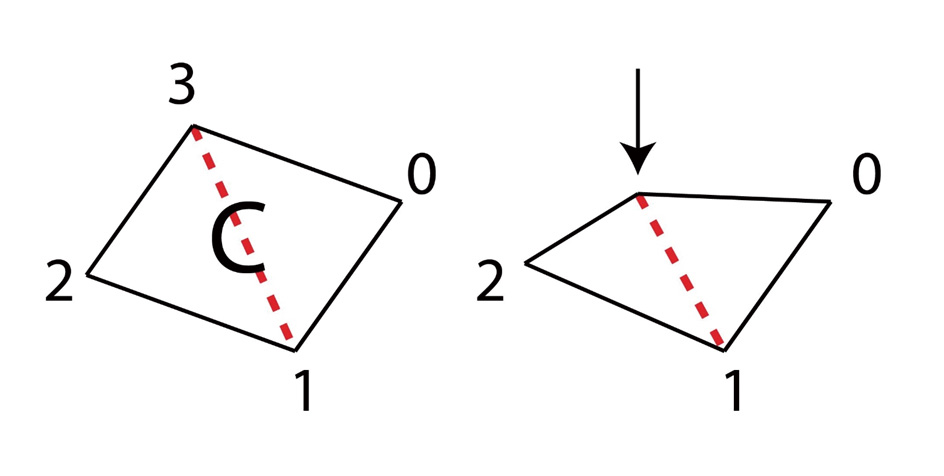
이제 전체적인 logic을 digital화 하기 앞서 모서리가 위를 향해 접히는 경우, 아래를 향해 접히는 경우 그리고 접히지 않는 경우를 어떻게 시뮬레이션할지 생각해 봅니다. 하나의 정사각형이 대각선을 중심으로 접히는 것은 공유하고 있는 변을 통한 hinge액션으로 이해될 수 있습니다. 이를 그림으로 나타내면 아래와 같습니다. 즉 B의 경우는 0번째와 2번째를 이어주는 선분을 공유하며 모서리가 종이면의 아래 방향으로 향하도록 접하고 C의 경우는 1번째와 3번째를 이어주는 선분을 공유하며 모서리가 종이면의 아래 방향으로 향하도록 접힙니다(Fig. 4).
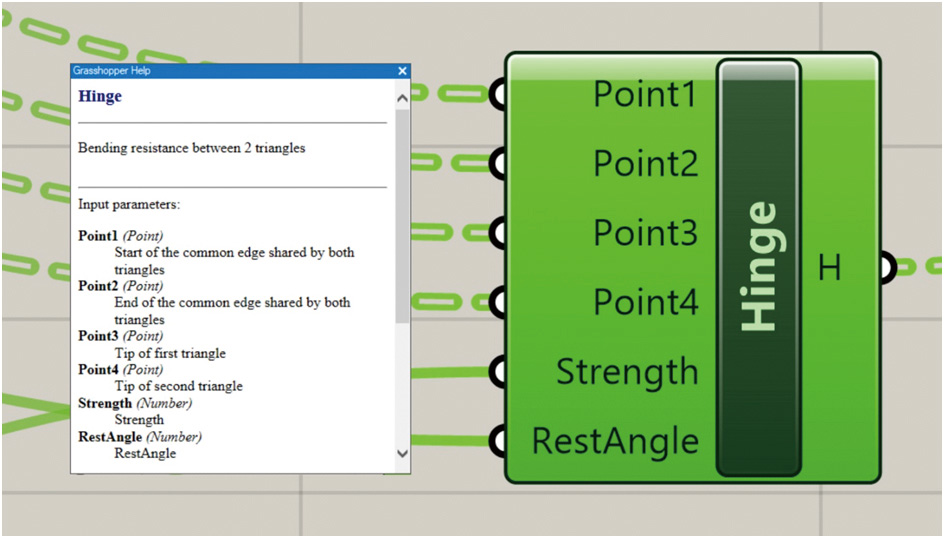
Grasshopper / Kangaroo의 hinge는 다음과 같은 parameters를 요구합니다(Fig. 5). 첫 번째 점은 공유하는 변을 시작하는 점이고 두 번째 점은 공유하는 변이 끝나는 점, 세 번째 점은 첫 번째 면의 다른 한 점(삼각형이라 가정했을 때), 네 번째 점은 두 번째 면의 다른 한 점 입니다. 이를 바탕으로 해당하는 점 input parameter들에 각 unit의 해당하는 점을 넣어 주면 됩니다. Rest angle은 종이가 접혔을 경우에 해당하는 일종의 평형상태의 각도입니다. 이 각도는 0에 가까운 숫자를 넣어주면 되지만 이 각도와 접히는 선분의 방향에 따라 위로 접히는지 아래로 접히는지가 결정됩니다.
다시 말해 아래 그림에서 공유하는 선분이 점 1에서 3으로 정의되었고 점 0이 첫 번째 삼각형을 구성, 점 2가 두 번째 삼각형을 구성한다면 2°의 rest angle은 공유하는 선분을 중심으로 오른손 법칙에 의해 첫 번째 삼각형으로부터 2°의 각도를 유지하는 평형상태에 도달하게 됩니다. 이는 보는 각도에 따라 공유하는 모서리가 위로 올라오는(혹은 아래로 내려가는) 경우를 나타냅니다. 반대로 -2°의 rest angle은 공유하는 선분을 중심으로 오른손 법칙에 의해, 첫 번째 삼각형으로부터 -2°의 각도를 유지하게 되므로(358°를 회전하게 되므로) 보는 각도에 따라 공유하는 모서리가 아래로 내려가는(혹은 위로 올라오는) 경우를 나타냅니다(Fig. 6).

다음 회에서는 이를 scripting하는 과정을 간략히 살펴 보도록 하겠습니다.
글. 성우제 Sung, Woojae 세종대학교 건축학과 조교수
www.woojsung.com, www.selective-amplification.net
'아티클 | Article > 칼럼 | Column' 카테고리의 다른 글
| 살아 숨 쉬는 건축여행 ⑥예산 시가지 발달과 예산의 발전 2022.11 (0) | 2022.11.10 |
|---|---|
| 입춘대길 2018.02 (0) | 2022.11.09 |
| 시카고의 트럼프 스마트 팩토리 _ 바르코우 라이빙거 2018.02 (0) | 2022.11.09 |
| 서양 건축미 개념의 역사적 전개 연구 (2) _ 아네르 테트라고노스와 아르카디아 2018.02 (0) | 2022.11.09 |
| 무술년이 밝았습니다 2018.01 (0) | 2022.11.07 |
