2022. 12. 1. 10:08ㆍ아티클 | Article/칼럼 | Column
Parametric DesignⅩⅨ
지난 시간에 말씀드렸듯이 오늘은 지난 2회에 걸쳐 고안된 종이접기의 방법을 paramtric tool을 이용하여 digital model화 하는 과정에 대해서 알아보도록 하겠습니다. 사용된 툴은 Rhino 3d, Grasshopper 및 Kangaroo Physics입니다.
먼저 전체적인 구성을 살펴보자면, 세 가지 주요 구성 요소가 있습니다. (fig. 01). 첫번째는 초록색으로 표현된 Rhino 3d로부터의 입력값을 필요에 따라 재가공하여 선택적으로 추출하는 과정입니다. 그리고 붉은 색으로 표현된 부분에서는 이렇게 선별적으로 추출된 값을 이용하여 종이접기라는 특정 행동을 모사하는 한정적 거동상의 특징을 기술합니다.
1) 종이의 특성상 접히는 삼각형 / 사각형의 변의 길이는 변하지 않으며,
2) 개별적으로 쪼개어진 면들이 접히는 것을 시뮬레이트 하기 위해 각 인접한 패널들이 0도에 근접한 각도를 향해 접혀서 안착하도록 하며,
3) 이러한 과정 중 각각의 삼각형 / 사각형 면들은 뒤틀리지 않은 평평한 면을 이루도록 합니다.
세번째로 푸른색으로 표현된 부분에서는 상기한 거동상의 특징을 이용하여 Kangaroo Physics를 이용하여 실제 시뮬레이션이 일어나도록 합니다. 그 이외의 부분들은 각 컴포넌트들을 이어주기 위한 과정들, 혹은 이를 화면상에 나타내기 위한 과정들입니다.
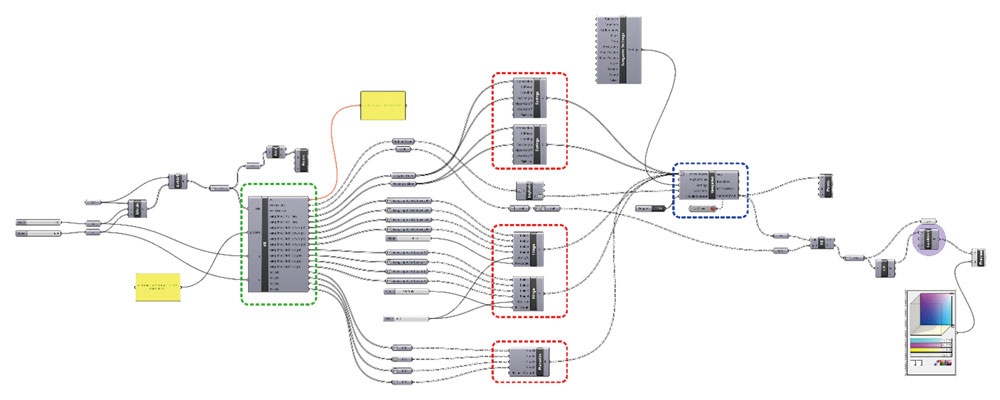
첫번째 부분을 먼저 살펴보겠습니다. (fig. 02). 화면의 우측으로 보이는 영역에서는 divide component를 이용하여 시스템의 전체를 구성하는 큰 면을 5x6의 그리드로 쪼개게 됩니다. 그리고 노란색으로 표현된 부분은 지난 2회에 걸쳐서 정의된 접힘의 패턴을 나타내는 문자 열입니다. Grasshopper가 하나의 조각난 면을 process할 때마다 해당 위치의 문자코드를 참조하여 면이 위로 접힐지 아래로 접힐지, 아니면 접히지 않을지에 대해 판단을 하게 해줍니다. 그리고 마지막으로 오른쪽에는 visual basic으로 만들어진 component가 위치하게 되는데요, 이는 주어진 input geometry를 각 요소별로 분해를 하고 이를 이용하여 종이접기라는 특정 행동의 거동을 모사할 수 있도록 digital model 을 생성하는 매개변수로 사용하게 됩니다.
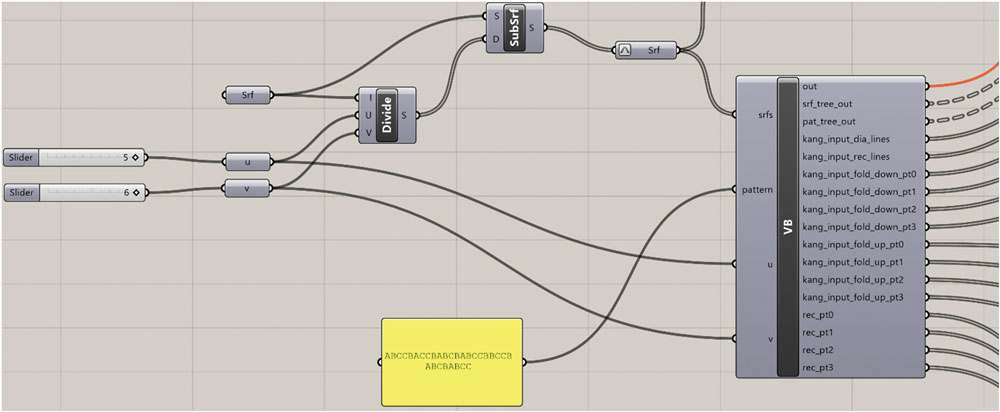
Visual Basic component의 입력값은 상기 기술했듯이 기준면(srfs), pattern, u and v로 구성됩니다. 기준면은 Rhino 3d 상에 존재하는 면이며 전체적인 시스템의 크기를 결정합니다. Pattern은 아래의 그림에서와 같이(fig. 03) 해당 면이 접히는 방향을 미리 설정하여 이를 grasshopper에 통보하는 역할을 하게 됩니다. U와 V는 기준면이 작은 면으로 분할되는 개수를 의미하여 우리의 경우는 30개의 면으로 분할됩니다.

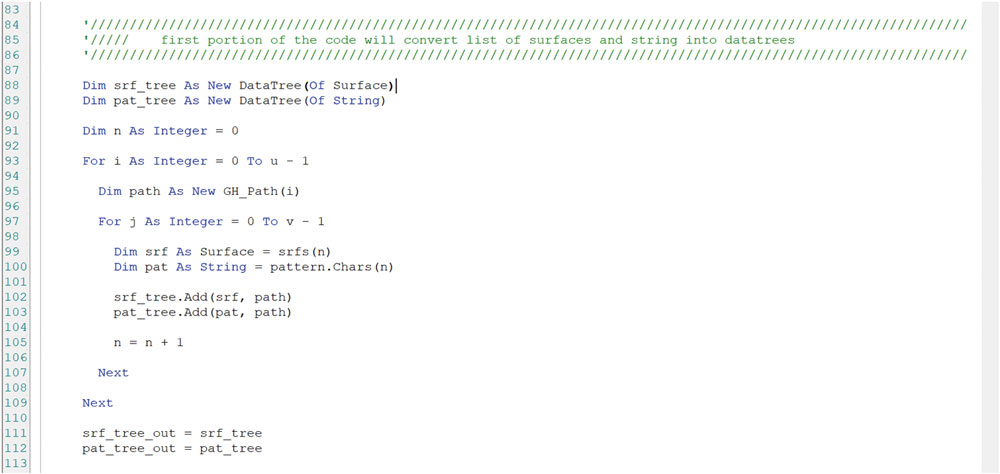
이제 visual basic의 각 부분들을 살펴보도록 하겠습니다. 첫번째 파트에서는 rhino로부터 1차원 array형태로 전달된 30개의 나뉘어진 면들을 grasshopper의 tree data structure로 전환하는 과정입니다. Tree data strcuture는 다차원의 array로 볼 수 있는데요. 쉽게 이해하기 위해 윈도우나 맥의 폴더 구조를 생각하면 될 것 같습니다. 동일한 폴더 및 하위 폴더의 구성을 가지고 있는 순차적인 다른 이름의 폴더들이 병렬로 존재하고 그 폴더 구조상 제일 깊숙한 곳에 위치한 단일 혹은 복수의 파일들은 해당 파일을 주소만을 알게 됨으로써 손쉽게 접속이 가능하게 됩니다. 이러한 병렬적인 특성으로 인해서 하나의 알고리듬을 생성한다면 이를 병렬로 구성된 다수의 지오메트리에 적용할 수 있게 됩니다. 앞서 말했듯이 각각의 면에 면이 접히는 방향성을 지정하기 위해 두개의 동일한 data tree를 구성하고 하나에는 해당 면을 다른 하나에는 면접기의 패턴을 입력해주게 됩니다. 주어진 면과 패턴이 1차원 array였으므로 두개의 for~next 문을 이용해서 병렬의 구조로 재구성하게 됩니다. 두개의 for~next를 사용하는 이유는 조금더 직관적으로 개별 면들의 위치를 파악하기 위해 5X6의 좌표체계를 차용하기 위함입니다(fig. 04).
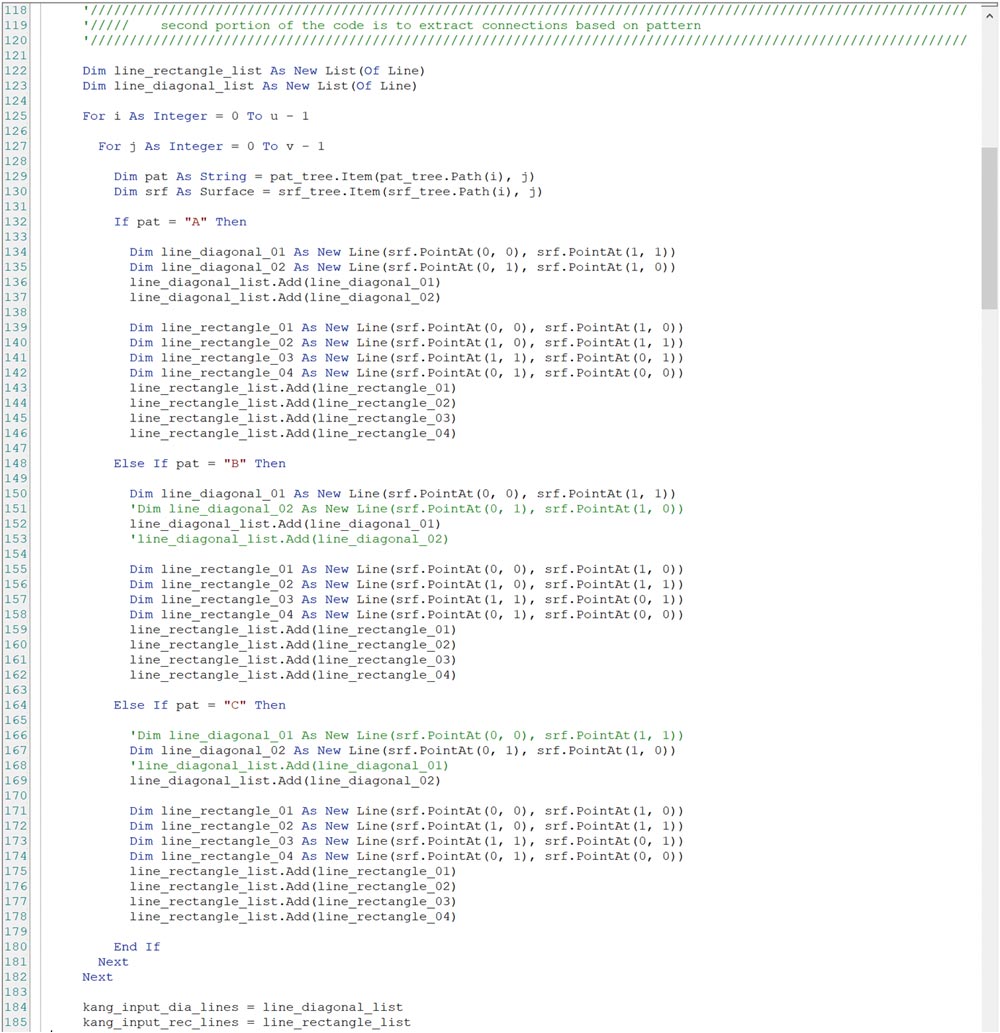
다음으로는 이렇게 구성된 두개의 dataset을 하나하나 확인해 접기의 패턴별로 해당면으로부터 필요한 정보를 선별적으로 추출하는 과정입니다. 즉 패턴 A일 경우는 접히지 않는 면이기에 평평해야 하므로 네 개의 외곽선분과 두개의 대각선을 추출하고 이를 면을 평면으로 유지하는 데에 쓰이게 됩니다. 뒤에 조금 더 자세하게 다루겠지만 네 개의 변이 같은 길이가 되는 것 만으로는 해당 사각형이 평평하다고 장담을 할 수 없게 됩니다. 하지만 네 모서리를 연결하는 두 개의 대각선이 같은 길이가 된다고 하면 이 사각형은 평평하다고 가정할 수 있습니다. 비슷한 논리로 패턴 B와 C의 경우는 특정한 대각선의 방향으로 접혀야 하므로 패턴A의 경우에 비교하여 하나의 대각선이 항상 같은 길이일 필요성이 없어지게 됩니다. 이에 패턴 B와 C에서는 그 대각선을 추출하는 행이 주석 처리되어 실행되지 않도록 합니다(fig. 05).
지난 시간에 언급했던 hinge action부분은 조금 더 복잡한 설명이 필요하므로 다음회에 설명하도록 하고 순서를 건너뛰어 스크립트의 마지막 부분으로 가보겠습니다. 이 부분은 앞서 언급했던 면을 평평하게 유지하는 부분에 대한 추가적인 안전장치로 보면 되겠습니다.
즉 두개의 대각선과 네 개의 변의 길이가 같다라는 가정이 패턴 A를 가진 면의 평평성을 유지하게 하지만 추가적으로 Kangaroo에서 제공하는 Planarize라는 컴포넌트를 이용하면 좀 더 확실하게 면이 평평하다는 것을 보장할 수 있게 됩니다. 해당 컴포넌트는 다음회에 언급하겠지만 네 개의 꼭지점을 요구합니다. 이를 통해 네 개의 해당 점들로 이루어진 면은 평평하도록 Kangaroo에서 처리하도록 합니다. 이를 위해 패턴 A에 해당하는 면들은 네 개의 꼭지점을 추출하여 이를 별도의 data set에 저장하는 과정을 거치게 됩니다(fig. 06).

다음 회에서는 스크립트의 나머지 부분 및 이들이 어떻게 Kangaroo에 연결이 되는지에 대해 살펴보도록 하겠습니다.
글. 성우제 Sung, Woojae 세종대학교 건축학과 조교수
'아티클 | Article > 칼럼 | Column' 카테고리의 다른 글
| 인구 5만 지방중소도시의 상점가 재생 _ 미야자키(宮崎) 니치난시(日南市) 아부라츠(油津)상점가 2018.05 (0) | 2022.12.01 |
|---|---|
| 건축사라는 자부심 2018.04 (0) | 2022.12.01 |
| 바르셀로나의 CMT 회사 사옥/ 배틀 앤 로이그 아키텍츠 _ 엔리크 배틀, 후안 로이그 2018.04 (0) | 2022.12.01 |
| 협회가 잘해야 한다 2018.03 (0) | 2022.11.30 |
| 오키 사토와 넨도 Part II 2018.03 (0) | 2022.11.30 |
